티스토리 뷰
[Reels] The simple theoretical background of Domain generalization
BayesianBacteria 2024. 4. 30. 00:46Here I introduce the generalization error bound of the Domain generalization problem, which is the test domain—or style, sometimes—differs from the training domain.

Preliminaries
Notations
- $X \in \mathcal{X} \subset \mathbb{R}^d, Y\in \mathcal{Y} \subset \mathbb{R}$ : Common input and target space
- $P^i_{XY}$: Data distribution of the i'th domain
- $S^i\sim P^i_{XY}$: Samples for the i'th domain
- $\epsilon^i$: Risk of the i'th domain
(Definition) Domain generalization
Assume that:
- Given M training (source) domains $S_{train}=\{S^i| i=1,\dots,M\}$
- The joint distribution between each pair of domains are different: $P^i_{XY} \neq P^j_{XY}, 1\leq i\neq j \leq M$
Then our goal is to learn a robust and generalizable function $h:\mathcal{X}\rightarrow \mathcal{Y}$ such that
$$ \min_h \mathbb{E}{(\mathbf{x},y)\in S_{test}} [l(h(\mathbf{x}),y)] $$
where $l$ is a loss function and $S_{test}$ is a target (unseen) domain.
(Definition) $\mathcal{H}$-divergence
The role of $\mathcal{H}$-divergence is to measure the how much different between two domains. The $\mathcal{H}$-divergence between domains $P^S_{X}$ and $P^t_{X}$ is defined as following:
$$ d_{\mathcal{H}\Delta\mathcal{H}}(P^s_X, P^t_X):= \sup_{h,h'\in \mathcal{H}} |\epsilon^s(h,h') -\epsilon^t(h,h')| $$
where
$$ \epsilon^s(h,h') = \mathbb{E}_{\mathbf{x}\sim P^s_X}[h(\mathbf{x})\neq h'(\mathbf{x})] = \mathbb{E}_{\mathbf{x}\sim P^s_X}[|h(\mathbf{x})- h'(\mathbf{x})|] $$
Here, $h, h'$ are any classifiers in $\mathcal{H}$, not typical trained-estimator with respect to empirical risk minimization.
However, directly accessing to the distribution of domain $i, P^i,$ is intractable, we can use the empirical$\mathcal{H}$-divergence using unlabeled data samples of the domain $i, \mathcal{U}^i$. Thus, the empirical$\mathcal{H}$-divergence between domains s and t is following:
$$ \hat{d}_{\mathcal{H}\Delta\mathcal{H}}(\mathcal{U}^s, \mathcal{U}^t):= \sup_{h,h'\in \mathcal{H}} |\epsilon_{\mathcal{U}^s}(h,h') -\epsilon_{\mathcal{U}^t}(h,h')| $$
where $\epsilon_{\mathcal{U}^s}$ is the empirical risk with the dataset $\mathcal{U}^s$.
Domain generalization error bound
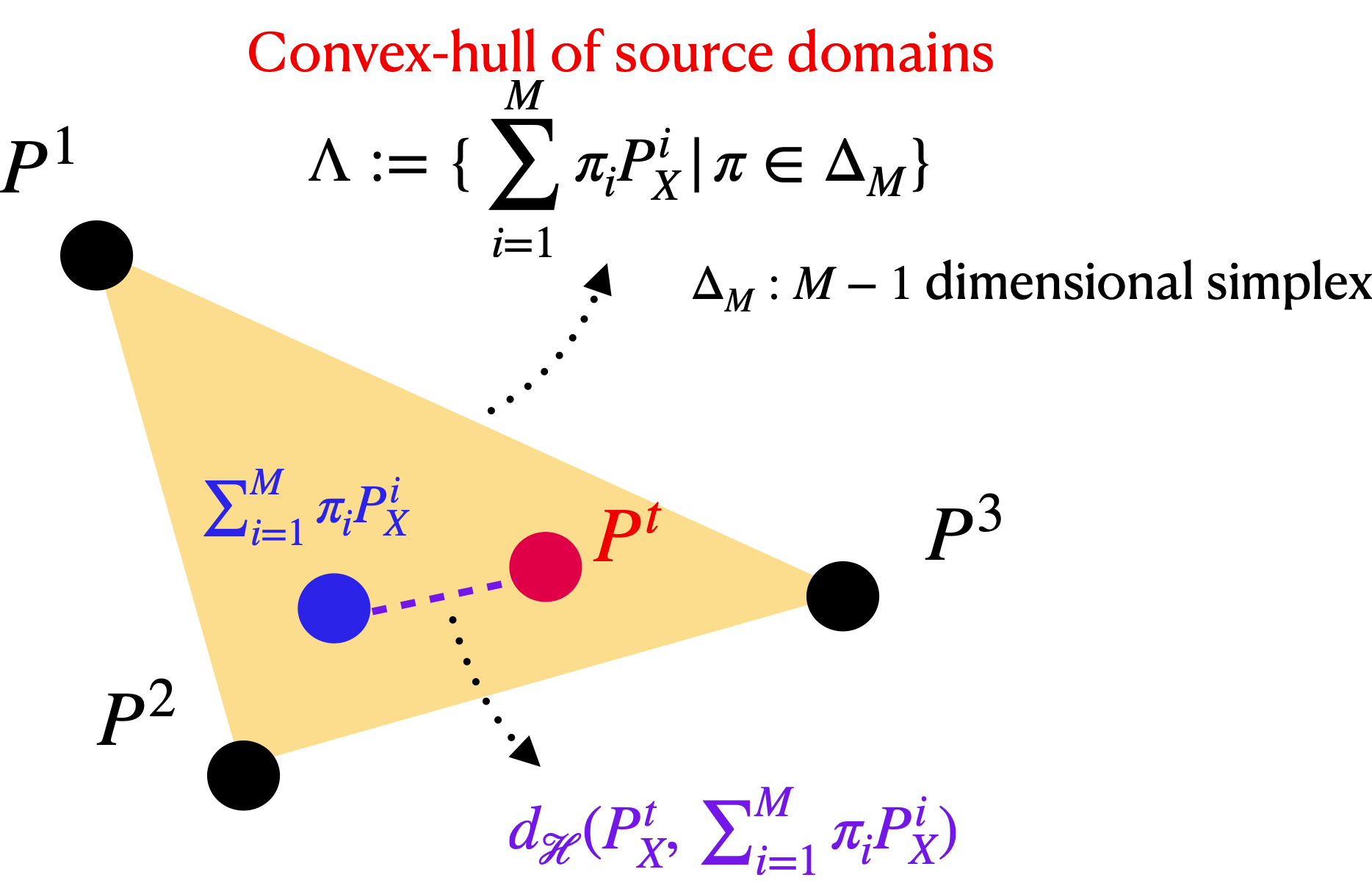
(Assumption) The target domain is in a convex hull of source domain distributions.
Let $\Delta_M$ is the $(M-1)$ dimensional simplex, then we assume that our target domain, $P^t_X$, is within the convex hull, $\Lambda := \{\sum_{i=1}^M \pi_i P^i_X | \pi \in \Delta_M\}$.
With the above assumption, following theorem holds.
(Theorem) Domain generalization error bound.
Let $\gamma:=\min_{\pi \in \Delta_M} d_{\mathcal{H}}(P^t_X, \sum^M_{i=1}\pi^*_i P^i_X)$ with minimizer $\pi^*$ be the distance of $P^t_X$ from the convex hull $\Lambda$, and $P^X:=\sum^M_{i=1} \pi^*_i P^i_X$ be the best approximated within $\Lambda$. Let $\rho:=\sup_{P'_X,P''X \in \Lambda} d_{\mathcal{H}}(P'_X, P''_X)$ be the diameter of $\Lambda$. Then it holds that:
$$ \epsilon^t (h) \leq \sum^M_{i=1} \pi^*_i \epsilon^i(h) + \frac{\gamma + \rho}{2} + \lambda{\mathcal{H},(P^t_X,P^*_X)} $$
where $\lambda_{\mathcal{H},(P^t_X,P^s_X)}$ is the ideal joint risk across the target domain and the domain with the best approximator distribution $P^*_X$.
$$ \lambda_{\mathcal{H},(P^t_X,P^X)} = \inf_{h \in \mathcal{H}}\mathbb{E}_{(\mathbf{x},y)\sim P^X} [l(h(\mathbf{x}),y)] + \mathbb{E}_{(\mathbf{x},y)\sim P^t_X} [l(h(\mathbf{x}),y)] $$
What this theorem states?
The above theorem gives us insights of several ways to reduce domain generalization error.
- Reducing each risk of domains can reduce the bound ($\epsilon^i$).
- If the target domain $,P^t$, can be easily approximated by the mixture of the source domains, the bound is tigthened. ($\gamma$)
- Reducing the distance between the source domains can reduce bound. ($\rho$)
(1) motivates us to learn well-generalized models for each domain; (2) and (3) motivate us establishing domain-invariant representation.
Note that $\epsilon^i$ is not a empirical risk of the domain $i$.
Limitation of the theorem
(Personal opinion) I do not think that the within-convex hull assumption is reasonable. If we have a domain that is far enough from the target domains, is it possible that the target domain $P^t$ could be outside of the convex hull?
However, if we consider that the outside of the convex hull as "completely different task" for the source domains, it may be a reasonable assumption. For instance, if we consider an animal-image classification task, it makes sense that the target domain is cartoon images of dogs. But the cartoon images of refrigerators, are not even our objective of the model, the animal-image classification. Generously speaking, this can be an example of the "outside of the convex hull", which implies a completely different task.
'Showing off studying ML > ML - academic reels' 카테고리의 다른 글
| [Reels] LCM-Lookahead for Encoder-based Text-to-Image Personalization (2) | 2024.10.15 |
|---|---|
| [Reels] Imagen yourself (0) | 2024.10.15 |
| [Reels] Battle of the Backbones: A large-Scale Comparison of pre-trained models across computer vision tasks (1) | 2024.08.20 |
| [Reels] HyDE (Hypothetical Document Embedding) (0) | 2024.05.02 |
- Total
- Today
- Yesterday
- generativemodeling
- domaingeneralization
- multiheadattention
- 몽중식
- loss-weighting
- DeepLearning
- Theme
- 이문설농탕
- vscode
- LLM
- Transformer
- 프렌밀리
- diffusion
- icml2024
- flowmatching
- deeplearning4science
- MachineLearning
- ICML
- finetuning
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
