티스토리 뷰
HiRA: parameter efficient Hadamard high rank adaptation for Large Language Models
BayesianBacteria 2025. 2. 11. 11:36ICLR2025
논문의 내용과 상관없이, 제가 이야기해보고 싶은 부분은 이탤릭체로 남깁니다.
texts with Italic represent parts that are not the part of the original paper, but rather my personal thoughts or additions
Limitation of the LoRA
- LoRA and most of its variants do not perform well when applied to complex tasks—such as commonsense reasoning.
- This degradation might be inevitable since the additional trainable parameters are “lower-rank” matrices.
Goal: Achieve a higher-rank adaptation for LLMs under the PEFT (parameter-efficient-fine-tune) strategy.
Motivation: recap the goal of PEFT
- PEFT requires a careful balance between model expressiveness and computational efficiency.
- Or, additionally, PEFT may help to prevent catastrophic forgetting of prior knowledge of models (https://arxiv.org/abs/2405.09673)
- (Observation 1) LoRA with higher ranks enhance peformance of Llama3-8B, implying the higher-rank adapatation offer significant advantages
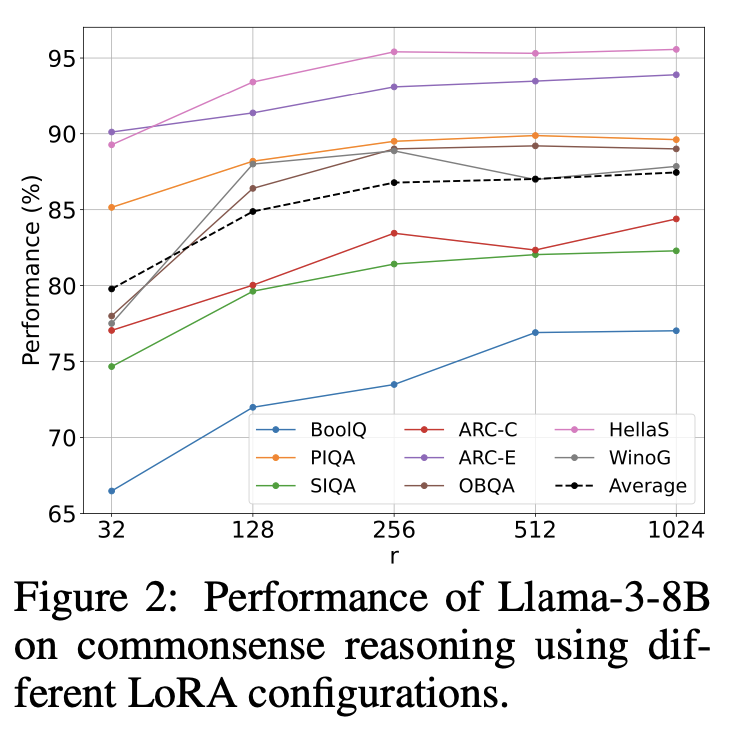
- However, increasing the rank in LoRA heightened computational budgets and it is difficult to train due to gradient explosion.
- We need an another and better tool for PEFT, but "higher-ranks"
HiRA in a nutshell: LoRA vs HiRA

Above Figure 3 is about everything of HiRA: trainable low-rank matrix A, B will be elementwisely multiplied with the original weight matrix (in other words, Hadamard product)
(Q: Connection with "Gated-Linear-Units" (GLU)-style activation): GLU activation functions has also similar structure with HiRA. $h(x) = f(x) \odot g(x)$ where $f$ and $g$ are some functions. The similar factor (Higher rank) is the main contribution of that GLUs outperforms other activations?
Why HiRA outperforms LoRA?
Simply put, the LoRA has lower "Rank". The property of the matrix rank is that the decompsed matrix $\Delta W = L_1 L_2$, where $L_1 \in \mathbb{R}^{d \times r}, L_2 \in \mathbb{R}^{r\times k}$ for $r < d, k$, has $\r$ rank. It may limit its capability to capture high-rank updates (it could be the complex tasks, such as reasoning of LLMs).
However, HiRA is free from such degradation due to the lower rank. HiRA utilizes the Hadamard product (element-wise product). And crucial benefit of using Hadamard product ($\odot$) is that the rank of the result matrix $P\odot Q$ is:
$$Rank(P \odot Q) \leq Rank(P) \times Rank(Q)$$
It is much larger (in the most of practical scenarios) than the rank of matmul utilized by LoRA:
$$Rank(PQ) \leq \min(Rank(P), Rank(Q)$$
Above just states upper bound of the rank. However, they empirically found that the Hadamard product could enhance the rank like belows:

HiRA even can have higher rank than the original weight matrix
Consider below the additional weight, $\delta W$, which becomes part of the PEFT $W_{\text{new_weight}} = W_{\text{original}} + \Delta W$:
$$\Delta W = W_{\text{original}} \odot W_{hi}$$
here, $W_{hi}$ is the NEW trainable parameter. With inequality of the above---Rank of Hadamard product---, rank of $\Delta W$ is bounded as below:
$$Rank(\Delta W) \leq Rank(W_{\text{original}}) \times Rank(W_{hi})$$
Therefore, the rank of additional weight what we newly train possibly exceeding the rank of original matrix. And, importantly, it is still computationally efficient---equivalent to that of LoRA---if we decompose $W_{hi}$ with $W_{hi} = AB$ where $A$ and $B$ is low-rank matrices. And of course, the additional weights can be merged into the original weights just like LoRA.
Intrinsic dimensionality, expressive power: Does higher rank for finetuning make sense?
Intrinsic dimensionality and matrix rank
Several works have shown that LLMs have a low intrinsic dimensionality, stating only small subsets of parameters is necessary for fine-tuning. LoRA is grounded for this discovery. Contrary to this, HiRA use higher rank trainable paramater. Does it make sense?
The answer is yes. Intrinsic dimensionality only consider the number of parameters and the small number of parameters does not inherently mandate low rank. It is not paradox.
(Does low number of parameters and high expressive power---In here, this was represented by rank of weights---is the key of the fine-tuning? or beyond that, is it the key of the model-design?) I guess not. Deep learning architectures have been developed from poor inductive bias to calibrated inductive bias. For instance, we experienced MLP to CNN: MLP has higher expressive power than CNN but function space of CNN is much more suitable for computer vision task than that of MLPs.
Not sure for fine-tuning regime. Once we choice the model architecture with nice inductive bias, low number of parameters and high expressive power rules might work?
Formal analysis of expressive power of HiRA, and the role of the original weight
The author also give formal analysis of the expressive power of HiRA. They define the expressive power as the minimal difference between the updated weight (the additional weight is added to the original weight) and its optimal parameter update (following previous work). The lower minimal difference to optimal value, the higher expressive power. For LoRA, this is equal to the (r + 1)-th largest singular value (where r is the rank of original weight matrix).
With the above definition of the expressive power, it is bounded to the singluar value and original weight (unlike LoRA, only depended on the singluar value of original weight) like below:

However, the role and contribution of the pretrained weight $W_0$ is somewhat unclear. They claimed that $W_0$ serves a dual role for both confining and facilitating the adaptation. It may be due to limiting the flexibility to reduce expressive power with $\sigma_{r+1}(\bar{E} \oslash W_0)$---since it might reduce the singular value?
Gradient analysis: gradient exploits the prior knowledge of the original weight
Author also claimed that training HiRA surpass LoRA since it leverges the information encoded in the original weight $W_0$. This encoding might be explained by considering the gradient of lower rank matrices contains the $W_0$, unlike LoRA:
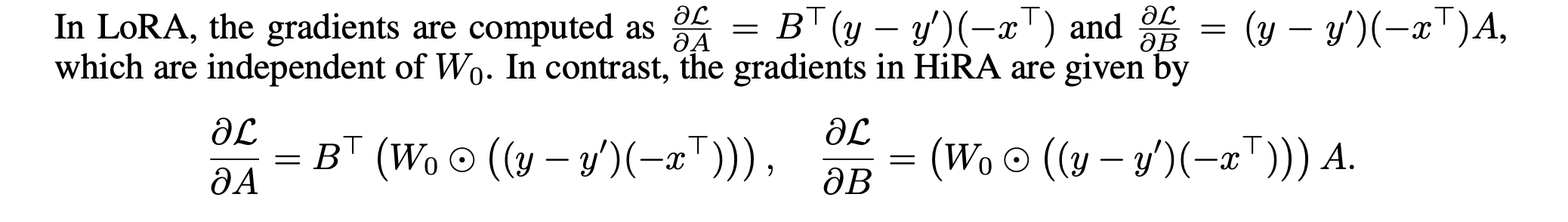
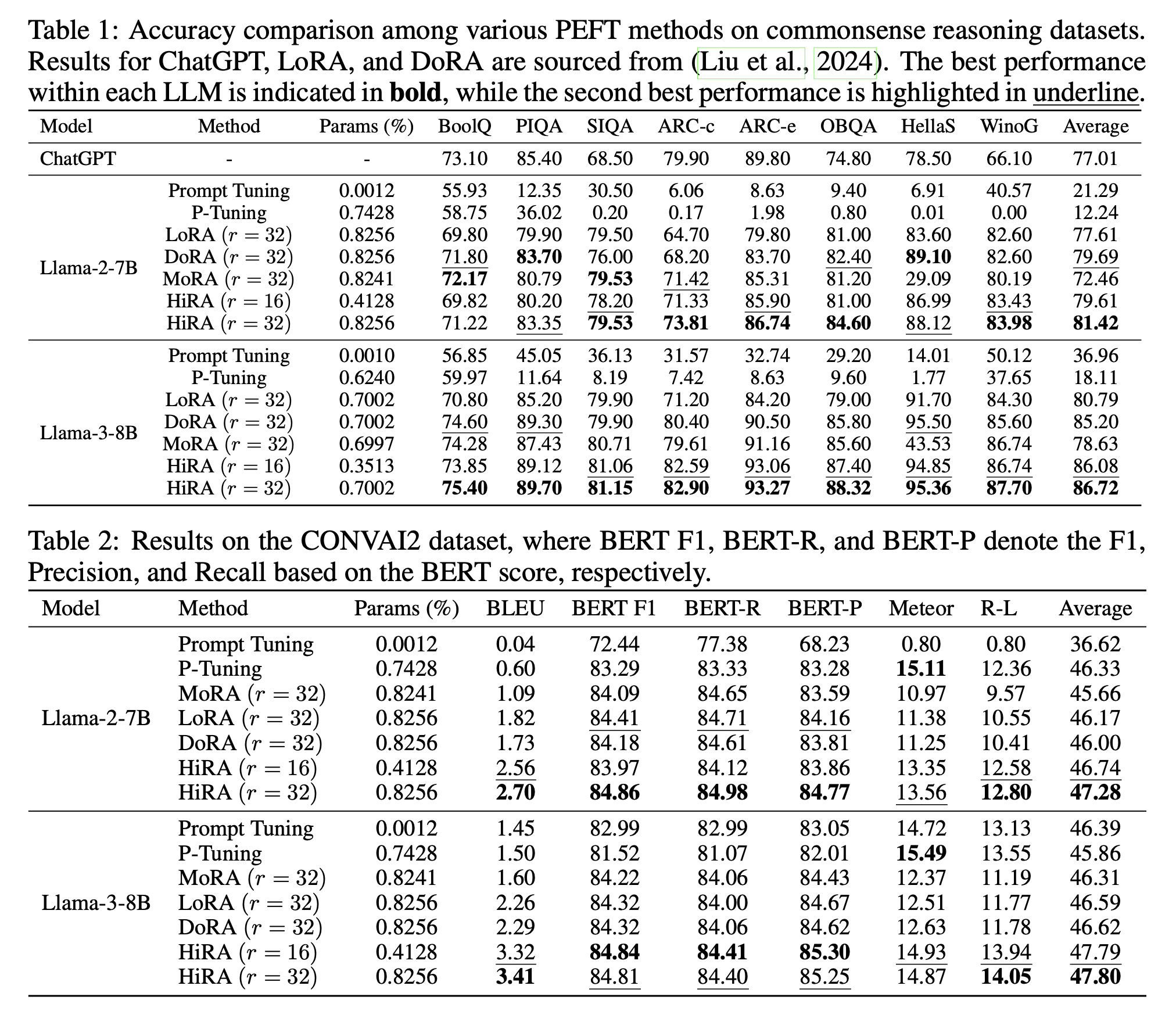
Experiments
(1) It outperformed LoRa, DoRA, MoRA in the various task
Especially for mathematics (GSM8K), which may be relatively requiring complex reasoning.

(2) Singular value scales of HiRA somehow is well-matched that of Full-Fine-Tuning (FFT)

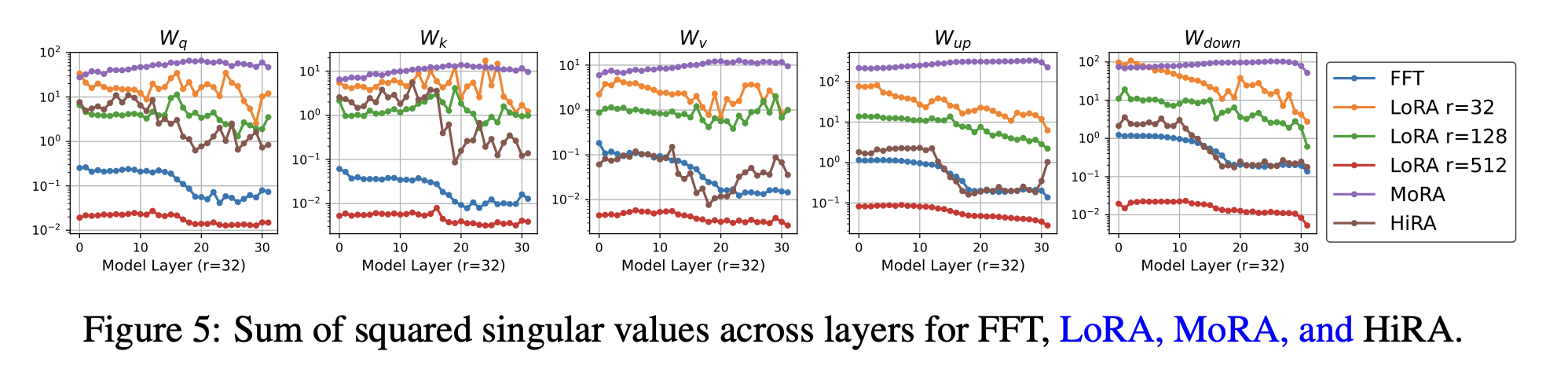
If we consider the singular value scale (its norm of the counts of larger singular value in the weight) indicates the expressive power of the model, HiRA is in the "high, but not dangerously high" zone. For instance, MoRA tends to be larger singular values and their counts are also high may increase the risk of forgetting. The only small number of singular values of LoRA mainly contribute (in other words, high norm). Unlike them, HiRA has proper number of large-singular values and their norms. Well-matched with FFT supports this claim.
(3) $W_0$ may contributes the fine-tuning
They explore the impact of different choice of $R$ in $\Delta W = R \odot W_{hi}$ (for the original choice, $R=W_0$, the pretrained weight). if the $W_0$ is replaced with $R$, the finetuning is doomed. This may highlights $W_0$ plays a key role for HiRA fine-tuning by conveying useful information from pretrained weight, as they claimed.

(4) HiRA works best to apply for both fully-connected layers and QKV of transformers.

(Q) LoRA has same tendency or not?
(5) Interestingly, hybrid approach (LoRA + HiRA) works

Authors also demonstrates usefulness of LoRA + HiRA: $W_0\odot A_{hira}B_{hira} + A_{lora}B_{lora}$ is added into the original pretrained weight $W_0$. Furthermore, they claimed that table 6 shows that the higher rank of HiRA is preferable over LoRA since higher $r_1$ achieve the best score.
On the "forget-less" benefit
Recently, (Biderman et al., 2024) have shown that although LoRA fine-tuning underperform full-finetuning, it is better maintaining the performance of base model on tasks outside of the target domain. It suggests that there is a tradeoff between preserving original information of the pretrained model (or, knowledge of it) and adaptation of the target task.
The below figure from the Biderman's paper is a proper example to show such tradeoffs. Y axis represents the target task the model newly learns, and the X axis represents the other tasks that pre-trained model already learned.

Full-fine tuning and higher rank of LoRA can achieve the higher accuracy on the target task, but they sacrifice the prior knowledge of the pre-trained weight (HellaSwag, ARC-challenge, WinoGrande here). If so, a question naturally arises: Can HiRA achieve a better Pareto front for the forgetting-adaptation trade-off? If it can, I believe this would be another significant contribution of HiRA. If it can not, it still has the benefits to acquire full-finetuning-level expressive power despite of its computational-efficiency. Exploring LoRA-level-efficienchy and full-finetuning-level-expressive-power methods for the forgetting-adaptation trade-off could be valuable research direction.
'Showing off studying ML > ML - 특집' 카테고리의 다른 글
| Extracting a secret sauce from Meta MovieGen (7) | 2024.10.17 |
|---|---|
| Vision transformers need registers (1) | 2024.08.23 |
| 메타분석 시리즈: Loss re-weighting before and after the era of LLMs (2) | 2024.08.13 |
| Improving Transformers with Dynamically Composable Multi-Head Attention (0) | 2024.07.09 |
| Komolgorov-Arnold Network (KAN) (1) | 2024.06.11 |
- Total
- Today
- Yesterday
- deeplearning4science
- Theme
- 이문설농탕
- loss-weighting
- MachineLearning
- vscode
- LLM
- 몽중식
- icml2024
- DeepLearning
- multiheadattention
- domaingeneralization
- diffusion
- Transformer
- finetuning
- 프렌밀리
- ICML
- flowmatching
- generativemodeling
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
